KL Diversion ＆ JS Diversion

简介

KL散度和JS散度本质上都是用于用来衡量两个分布之间的差异的值，并且分别具有一些不一样的性质，并且通常它们分别对应用于解决一些不一样的实际问题。

这篇文章从信息论和熵为起点，展开对 KL Diversion 和 JS Diversion 的介绍。

1 信息论

自信息量定义：

对于事件集合$X=\left\{x_{1}, x_{2} \ldots x_{n}\right\}$，其中某一事件$x_{i}$发生的概率为$p_{i}$，则自信息量定义为：

$$I\left(x_{i}\right)=-\log p_{i}$$

（通常log底数取2，单位为bit）

自信息的理解

对于自信息这个概念，可从多个角度来理解：

• 表示事件不确定性的大小；
• 表示事件发生带来信息量的多少，事件一旦发生，就消除了不确定性，从而带来了信息量；
• 表示为了确定事件的发生，所需信息量的多少。

2 熵

熵，又叫平均自信息，数学定义如下：

$$H(X)=E\left(I\left(x_{i}\right)\right)=-\sum_{i=1}^{n} p_{i} \log p_{i}$$

熵的理解

同样可以从多种角度理解熵的概念：

• 随机变量不确定性的大小
• 观测这个随机变量得到平均信息量的大小
• 确定这个随机变量取值所需的平均信息量大小
• 系统的凌乱程度

---

3 Divsersion

在机器学习中，p往往用来表示样本的真实分布，q用来表示模型所预测的分布，那么KL散度就可以计算两个分布的差异，也就是Loss损失值。

3.1 KL Diversion（相对熵）

Kullback-Leibler Diversion的作用：用分布q描述分布p时损失的信息量的大小。

KL散度只是对我们的熵公式的略微修改，考虑概率分布p及近似分布q。并且查看log值的差异：

$$D_{K L}(p \| q)=\sum_{i=1}^{N} p\left(x_{i}\right)\left(\log p\left(x_{i}\right)-\log q\left(x_{i}\right)\right)$$

本质上，我们用KL散度观察原始分布与近似分布之间的对数差的期望。

KL Diversion公式的改写

如果我们考虑log2，我们可以将其解释为“我们预计有多少比特位的信息丢失”，我们可以根据期望重写公式：

$$D_{K L}(p \| q)=E\left[\log p\left(x_{i}\right)-\log q\left(x_{i}\right)\right]$$

KL散度的两个特点：

• KL散度是不对称的
• KL散度不满足三角不等式

3.2 Cross Entropy（交叉熵）

$$\begin{array}{l} D_{K L}(p \| q)=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(\frac{p\left(x_{i}\right)}{q\left(x_{i}\right)}\right)=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(p\left(x_{i}\right)\right)- \\ \sum_{i=1}^{n} p\left(x_{i}\right) \log \left(q\left(x_{i}\right)\right)=-H(p(x))+\left[-\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(q\left(x_{i}\right)\right)\right] \end{array}$$

上述公式是对KL散度公式的整理，发现 KL散度=P的熵+交叉熵 。
因此在分类任务中，由于P的熵是定值，所以在一般的任务直接使用交叉熵作为Loss即可。

3.3 JS Diversion

JS散度度量了两个概率分布的相似度，是基于KL散度的变体，解决了KL散度非对称的问题。一般地，JS散度是对称的，其取值是0到1之间。定义如下：

$$J S\left(P_1 \| P_2\right)=\frac{1}{2} K L\left(P_1 \| \frac{P_1+P_2}{2}\right)+\frac{1}{2} K L\left(P_2 \| \frac{P_1+P_2}{2}\right)$$

JS Diversion的python实现

def JensenShannonDivergence(p, q):
    p = np.array(p)
    q = np.array(q)
    M = (p + q)/2
    return 0.5 * np.sum(p*np.log(p/M)) + 0.5 * np.sum(q*np.log(q/M))

3.4 Wasserstein距离

待更新。。。

4 参考资料

https://zhuanlan.zhihu.com/p/523745054——信息论

https://zhuanlan.zhihu.com/p/74075915——四种熵值

https://zhuanlan.zhihu.com/p/100676922——KL Diversion

https://zhuanlan.zhihu.com/p/34998569——当你对VAE中的知识有点模糊的时候可以回顾这篇文章

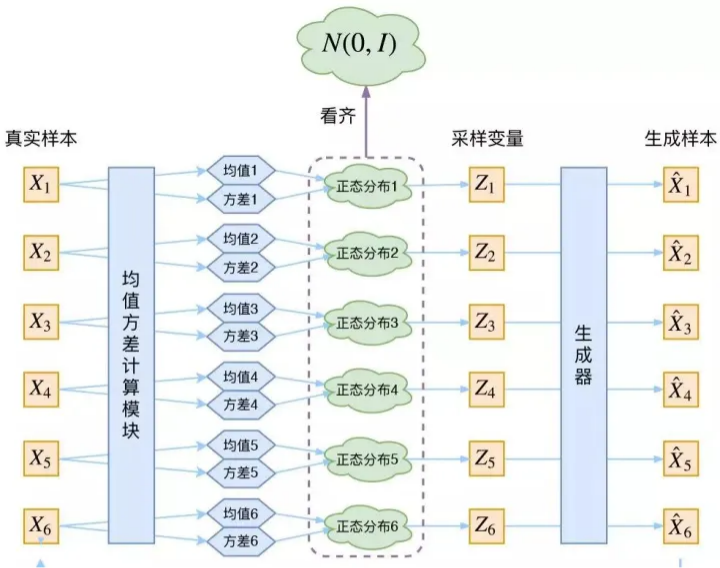
5 VAE-Model示意图